Volatility and Sharpe Ratio are inadequate financial measures
Example 1: daily lottery prized at $10'000
Imagine someone would offer you the following lottery.
This lottery has a minimum duration of 136 years (50'000 days). Therefore you will get a daily chance to win $10'000 on every day of your life for a single investment of only $500.
Would you accept this offer?
Imagine someone would offer you the following lottery.
- You have to put $500 in an account only once in your life.
- Every day $0,01 (1 Cent) will be deducted from your account.
- Every day you have 1:1000 chance to win $10'000.
This lottery has a minimum duration of 136 years (50'000 days). Therefore you will get a daily chance to win $10'000 on every day of your life for a single investment of only $500.
Would you accept this offer?
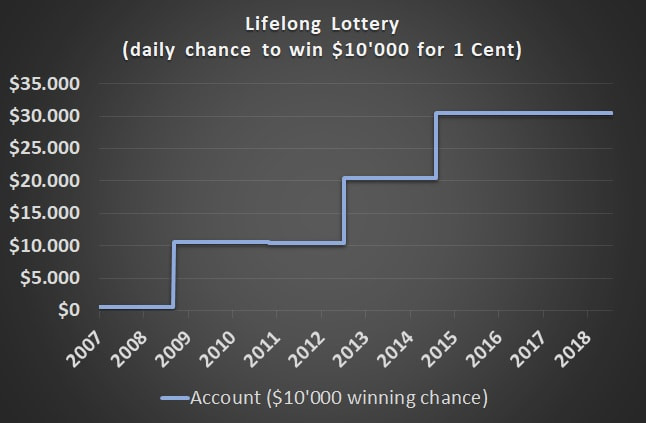
This charts illustrates how your account would have evolved during time. In regular frequency it would have increased in value by $10'000 since having a 1:1000 winning probability means that one wins every three years on average.
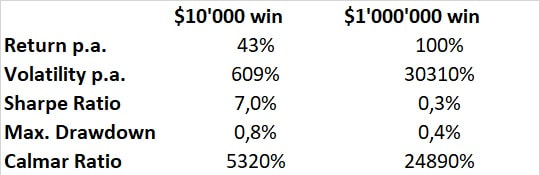
The metrics looks not as good as the chart, as long as you focus on volatility and sharpe ratio. During this 12 year period this strategy would have returned 43% p.a. while the volatility would have skyrocketed to 609%. Therefore the Sharpe Ratio with 7% is low compared to traditional asset classes like equity or bonds.
On the other hand, the Max. Drawdown is very low with a value of 0.8%. This leads to a sensational high Calmar Ratio of 5320% which is far beyond what traditional asset classes can deliver.
The metrics looks not as good as the chart, as long as you focus on volatility and sharpe ratio. During this 12 year period this strategy would have returned 43% p.a. while the volatility would have skyrocketed to 609%. Therefore the Sharpe Ratio with 7% is low compared to traditional asset classes like equity or bonds.
On the other hand, the Max. Drawdown is very low with a value of 0.8%. This leads to a sensational high Calmar Ratio of 5320% which is far beyond what traditional asset classes can deliver.
Example 2: Who wants to be a millionaire?
Sure, the volatility looks very bad in the example above. One could criticize that this example is just designed to make the volatility look bad. On the one hand, yes this example is designed. On the other hand, all strategies with a cash flow structure comparable to an insurance product have a pay off structure like the one from the example above. The volatility punishes strategy which allow for pay offs far beyond the average return, and what makes it worse - the volatility punishes beyond average surpluses exactly the same way as it punishes losses.
The upcoming example will show once and for all that volatility is an inadequate risk measure:
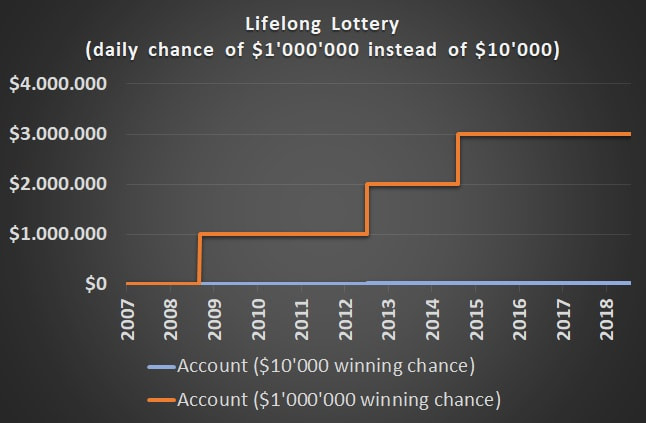
Now, a new lottery is offered to you which is exactly the same as the lottery you have just seen, except one thing: instead of having a daily chance to win $10'000 now you can win $1'000'000.
Sure, the volatility looks very bad in the example above. One could criticize that this example is just designed to make the volatility look bad. On the one hand, yes this example is designed. On the other hand, all strategies with a cash flow structure comparable to an insurance product have a pay off structure like the one from the example above. The volatility punishes strategy which allow for pay offs far beyond the average return, and what makes it worse - the volatility punishes beyond average surpluses exactly the same way as it punishes losses.
The upcoming example will show once and for all that volatility is an inadequate risk measure:
Now, a new lottery is offered to you which is exactly the same as the lottery you have just seen, except one thing: instead of having a daily chance to win $10'000 now you can win $1'000'000.
- You have to put $500 in an account only once in your life.
- Every day $0,01 (1 Cent) will be deducted from your account.
- Every day you have 1:1000 chance to win $1'000'000.
The volatility in the $1'000'000-lottery reaches a crazy 30310% compared to 609% before. The Sharpe Ratio diminishes to 0.3% from 7.0% in example 1.
An investor whose investment decisions are based on volatility and Sharpe Ratio would choose the $10'000-lottery over the $1'000'000. The Sharpe Ratio-investor does not want to be a millionaire.
It should be obvious to everyone that the right decision is to choose the $1'000'000-lottery. In contrast, the risk metric Max. Drawdown and the Calmar Ratio would lead an investor to make a reasonable decision.
An investor whose investment decisions are based on volatility and Sharpe Ratio would choose the $10'000-lottery over the $1'000'000. The Sharpe Ratio-investor does not want to be a millionaire.
It should be obvious to everyone that the right decision is to choose the $1'000'000-lottery. In contrast, the risk metric Max. Drawdown and the Calmar Ratio would lead an investor to make a reasonable decision.
Conclusion
Volatility as a risk measure is punishing deviations from a long-term average. It does not distinguish whether these deviations come from huge losses or huge profits. As a consequence all investment strategies which have an insurance-like pay-off are rated bad by the volatility.
In contrast, the Max. Drawdown is capable of measuring such strategies adequately. This is the reason, why I use the Max. Drawdown in all my strategy analysis tools to find successful systematic investment strategies.
In contrast, the Max. Drawdown is capable of measuring such strategies adequately. This is the reason, why I use the Max. Drawdown in all my strategy analysis tools to find successful systematic investment strategies.